Also: Potentiometers
What value is this resistor?
What does an X Ohm resistor look like?
How can I get a resistance of exactly X even though there are no commercial resistors of that value?
Resistors provide resistance in an electronic circuit. Without resistance, Ohms Law would not be usefull.
Many resistors are so small that it would be difficult to print their value and % tolerance on their body in digits. To overcome this, a coding system based on bands of distinctive colours was developed to assist in identification. Learning this ëcolour codeí is not as necessary as it used to be (thanks to accurate, low cost digital multimeters!), but itís not hard to learn and itís quite useful knowledge anyway.
The first thing to know is that in each decade of resistance ó i.e., from 10 - 100W, 100 - 1kW, 1k - 10kW, etc ó there are only a finite number of different nominal values allowed. Most common resistors have values in the ëE12í series, which only has 12 allowed values per decade. Normalised these are 1.0, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8 and 8.2. Multiples of these values are simply repeated in each decade ó e.g., 10, 12, 15, 18 and so on. Note that the ëstepsí between these values are always very close to 20%, because the E12 series dates from the days of resistors with ±10% tolerance.
To allow greater accuracy in circuit design, modern 1% tolerance resistors are made in a larger range of values: the ëE24í series, which has 12 additional allowed values per decade: 1.0, 1.1, 1.2, 1.3, 1.5, 1.6, 1.8, 2.0, 2.2, 2.4, 2.7, 3.0, 3.3, 3.6, 3.9, 4.3, 4.7, 5.1, 5.6, 6.2, 6.8, 7.5, 8.2 and 9.1. As before, these nominal values are simply repeated in each decade.
Resistors are sometimes packaged together into "networks" or collections of resistors in one physical package. There are two types:
Bussed: Bussed resistors are all connected on one side. These are typically used as pull up or pull down resistors, where the common point is connected to power or ground and the other side of each individual resistor is connected to a line on a "bus" of wires. This has the effect of biasing each of the bus wires to a known value. Typically, the first pin on the network is the common, and the other pins are the other end of each individual resistor. A bussed network resistor can be replaced by individual resistors, by simply connecting one side of each resistor to the common and the other side to the next line.
Isolated: Isolated resistors are just as the name implies; each resistor in the package is isolated from the next, and both side of each resistor is brought out to a seperate pin in the package. In this case, some care must be taken to understand the pinout of the network as there are different possible ways to bring out the pins. Still, replacement is simple once you have the internal schematic.
When indicated on a schematic, Resistors are often labeled by "R" and a number. E.g. R10 is the tenth resistor. The value will typically be specified with 2 or 3 digits of accuracy in engineering form (e.g. 2.3, 230 vice 2.3x102, or 43 vice 4.3x101), a multiplier (k, M, or none), and the Ohm sign. On European schematics, the Decimal point may be replaced with the multiplier and "R" used when no mutiplier is used. Eg 10R = 10 Ohms, 4M7 = 4.7 MOhms, 0R1 = 0.1 Ohms. In this case R10 may indicate a 0.10 Ohm resistor (in which case it should have been written 0R10) or (more likly) the tenth resistor on the schematic.
Resistors, along with all electronic components, are getting smaller these days. More and more are SMD and don't have much room for a label. So numeric codes are used instead. This code uses three numbers, sometimes followed by a single letter. The numbers are the significant digits and the decade. For example 102 is 1000 Ohms or 1K ohm. The 1 and 0 are the first two digits, then the 2 tells us to add 2 more zeros. 473 = 47k Ohms. A letter after the numbers gives the tolerance. M=±20%, K=±10%, J=±5%, G=±2%, F=±1%. Note that 012K is NOT a 12k Ohm resistor: the 01 is to be followed with 2 more zeros resulting in 0100 Ohms at 10% tollerance. Normally, however, a 100 Ohm resistor would be marked as 101K. If you read that wrong, it comes out to 101K ohms, which is not an allowed value in either E12 or E24.
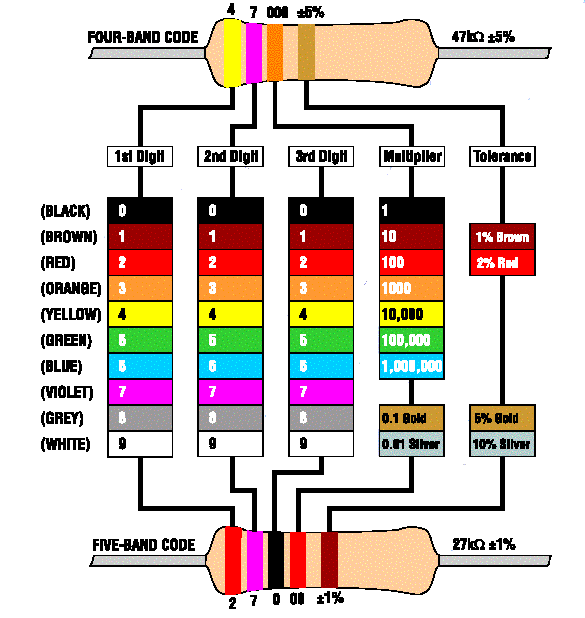
Most thru hole resistors are marked with a set of bands of different colors that encode numeric values. Typically, there are four bands. The first two bands are two digits of the value. The third band in the exponent or number of zeros to add to the value. The fourth band indicates accuracy using Red +/- 2% Gold +/- 5%, Silver +/- 10%, None +/- 20%. The values of the first three bands are color encoded as follows:
value color code menomic 0 Black BLK Black 1 Brown BRN Beans 2 Red RED Ripen 3 Orange ORG Over 4 Yellow YEL Yellow 5 Green GRN Grass 6 Blue BLU Before 7 Violet VLT Vinyards 8 Grey GRY Grow 9 White WHT Wine
There are various ways to remember the color codes. The one shown above is nice.
The next thing to know is that there are two different resistor colour coding systems in use: one using a total of 4 colour bands, and the other 5. The 5-band system is generally used for 2% and closer tolerance resistors, even though the 4-band system is quite capable of handling any resistors with E12 or E24 values. Both systems use the same band colours to represent the various digits; the main difference is that 5-band resistors have an additional ëthird bandí, which is almost always BLACK to represent a third digit of ë0í. Hereís how both systems work in practice:

4-band resistors will almost always have values in the E12 series, while 5-band resistors can have any value in the E24 series. This is worth remembering, because depending on the resistorís body colour, some of the band colours may not be easy to distinguish. Blue (6) and grey (8) sometimes look very similar, as do red (2), brown (1) and orange (3). So if youíre in doubt, check the apparent coded value against the allowed E12 or E24 values to see if itís ëlegalí ó or check with a digital multimeter, just to make sure.
Robert A. LaBudde, PhD, PAS, Dpl. ACAFS says:
The key to understanding resistor values is to realize they are almost always used in ratios, so equi-distribution in the logarithm is important.The "E6" series (1, 1.5, 2.2, 3.3, 4.7, 6.8) correspond to log10 values of 0.00, 0.18, 0.35, 0.52, 0.67, 0.83, which are a reasonably good approximation to 0/6, 1/6, 2/6, 3/6, 4/6 and 5/6.
The "E12" series adds 1.2, 1.8, 2.7, 3.9, 5.6 and 8.2. In log10 space, these are 0.08, 0.26, 0.43, 0.59, 0.75 and 0.91, which are reasonable approximations to the 12-ths.
The "E24" series expands the log10 fractions to 24-ths.
If you want the fewest number of values, use the E6 series. It gives the best resolution with 6 values.
If you want higher resolution, use the E12 series.
More important than the question of values, is the question of which decades to stock.
Here are a few rules:
- For low voltage needs (i.e., < 20 V), 1/4 W resistors are ideal.
- You will rarely use values below 100r, unless they're high wattage power types.
- You need a value to use for LED current limiting and pull-ups. I like using higher values, such as 2k2 or 4k7 to minimize power. Most modern LEDs light nicely with 2-3 mA of current, which is what you get with 2k2 @ 5V.
- You need 1M resistors for some common high-impedance purposes.
- You need resistors for setting op-amp gains or in voltage dividers. They should be in ratios of 1:3, 1:10, 1:30 and 1:100. They should not be too high, and not too low. I like 3k3, 33k and 330k. The 1:3 and 1:30 values can be achieved by adding 10k and 100k values.
- Every one seems to love decimal increments (they must count on their toes!). So 1k, 10k, 100k and 1M are very popular.
- You need some 47k values for input impedance for microphones, etc.
So, in summary, the following 1/4 W values would seem to be a minimal set:
330r, 1k, 3k3, 10k, 33k, 47k, 100k, 330k, 1M
Use the 330r or 1k for emitter bias.
Use the 1k or 3k3 for LED currents and pull-ups.
Use the 10k or 47k for microphone input impedance matching.
Use the whole set for gain setting and voltage dividers.
If you want to expand the set, start with 470r, 4k7 and 470k.
See also
Archive:
Questions:
| file: /Techref/resistors.htm, 12KB, , updated: 2016/8/12 17:22, local time: 2025/10/15 22:52,
216.73.216.114,10-3-244-150:LOG IN
|
| ©2025 These pages are served without commercial sponsorship. (No popup ads, etc...).Bandwidth abuse increases hosting cost forcing sponsorship or shutdown. This server aggressively defends against automated copying for any reason including offline viewing, duplication, etc... Please respect this requirement and DO NOT RIP THIS SITE. Questions? <A HREF="http://www.piclist.com/techref/resistors.htm"> Resistors</A> |
| Did you find what you needed? |
|
o List host: MIT, Site host massmind.org, Top posters @none found - Page Editors: James Newton, David Cary, and YOU! * Roman Black of Black Robotics donates from sales of Linistep stepper controller kits. * Ashley Roll of Digital Nemesis donates from sales of RCL-1 RS232 to TTL converters. * Monthly Subscribers: Gregg Rew. on-going support is MOST appreciated! * Contributors: Richard Seriani, Sr. |
Welcome to www.piclist.com! |
.