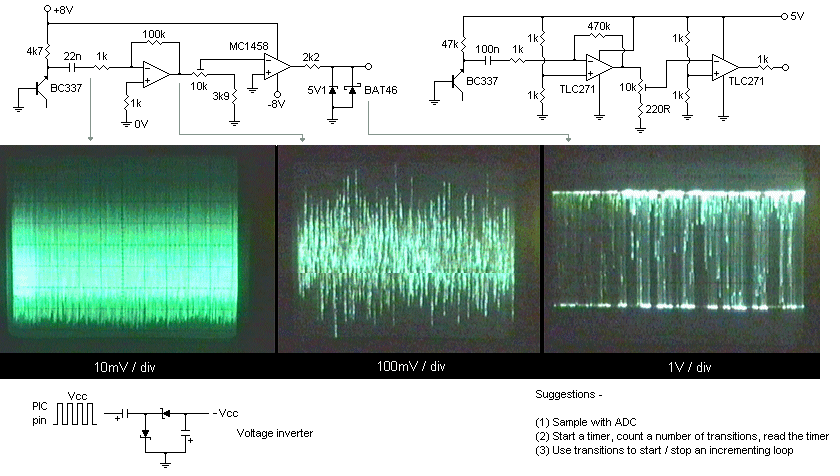
http://home.clear.net.nz/pages/joecolquitt/white_noise.html
Here's how to compute an 8-bit pseudorandom sequence. You can start with any value except zero and each time you run through the algorithm you'll get a new value.
- initialize a byte to any value except zero.
- calculate the sum (MOD 2) of bits 7, 1 and 0 of the byte.
- shift the byte 1 position to the left, shifting in the result of the above sum into bit 0.
- your byte now contains the random number (use this value to get the next one)
A (MOD 2) sum is the same as exclusive or (XOR).
This is an 8 bit LFSR (linear feedback shift register). If you want to design LFSRs of any number of bits, you might want to check out "Linear Feedback Shift Registers" by (who?) http://homepage.mac.com/afj/lfsr.html In particular the taplist http://homepage.mac.com/afj/taplist.html shows what bits to pick out, in order to get a "maximal length" of (2^n)-1 before it repeats.
So a maximal length 8 bit LFSR would repeat after all possible 255 values
and never hit 0. Unfortunately, a maximal length 8 bit LFSR requires either
4 taps or 6 taps. The above algorithm takes a short cut of using only 3 taps
-- "bits 7, 1, and 0". So it is *not* maximal sequence.
* Starting with "1", it repeats after 127 states.
* Starting with "2" (0000 0010), it repeats after 127 states (different than
the above).
* Starting with "0", it remains stuck at zero (like maximal length LFSRs).
* Starting with "FF", it remains stuck at "FF".
Maximal-length LFSRs always require an even number of taps. Some require the minimum of 2 taps, such as the ones for 3 bits, 4 bits, 5 bits, 6 bits, 7 bits, (but not 8), 9 bits, 10 bits, 11 bits, (bit not 12, 13, or 14), 15 bits, (but not 16), 17 bits, 18 bits, etc.
Design by Jinx, was approved for gaming by Internal Affairs Dept of NZ govt

http://home.clear.net.nz/pages/joecolquitt/white_noise.html
, design by dr. Imre Bartfai, 8/30/1999
+--------------------------------------------------------------------- Vdd
| 220k 220k 5V
| +---\/\/\---+ +---\/\/\---+------+
| | | | | |
| | |\ | | +------+ \
| EFT317 PNP +-----+----|- \ | | | / 220k
| C | | | >-+----| |----+ | |\ \
| |/ \ +-------|+ / 47n | +-----|- \ |
+--B| 220k / | | |/ | | | >--+
|\ \ | | 1/2 LM358 +----------|+ / |
|E | | | | | |/ \
+----| |----+--+ + + + / 47k
| 47n | | | | 1/2 LM358 \
\ \ \ \ \ |
4k7 / 1M / / 2k2 1M / / 2k2 + out
\ \ \ \ \
| | | | |
+-----------+-----+-----------------------+----+---------------- Vss
Standard TTL can not be driven, but CMOS (and maybe LS) are o.k.
The power supply must be filtered thoroughly due to the high gain!
See also:
Archive:
| file: /Techref/method/random.htm, 4KB, , updated: 2008/8/19 19:34, local time: 2025/10/21 23:03,
216.73.216.114,10-3-244-150:LOG IN
|
| ©2025 These pages are served without commercial sponsorship. (No popup ads, etc...).Bandwidth abuse increases hosting cost forcing sponsorship or shutdown. This server aggressively defends against automated copying for any reason including offline viewing, duplication, etc... Please respect this requirement and DO NOT RIP THIS SITE. Questions? <A HREF="http://www.piclist.com/techref/method/random.htm"> Random numbers, random, rnd</A> |
| Did you find what you needed? |
|
o List host: MIT, Site host massmind.org, Top posters @none found - Page Editors: James Newton, David Cary, and YOU! * Roman Black of Black Robotics donates from sales of Linistep stepper controller kits. * Ashley Roll of Digital Nemesis donates from sales of RCL-1 RS232 to TTL converters. * Monthly Subscribers: Gregg Rew. on-going support is MOST appreciated! * Contributors: Richard Seriani, Sr. |
Welcome to www.piclist.com! |
.