Micro controller interfacing to analog sensors
(such as the LM335A Temperature Sensor)

by James Newton

This page is about compexity and beauty in embedded engineering... or about units conversion maths and improving sensor accuracy with filtering and noise... or about building a digital thermometer using a temperature sensor connected to a microcontroller. As you wish.

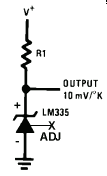
The LM335 is a magical bit of analog electronics, finely tuned to drop 10 milli-volts (0.01 volts) per degree C^ (or K^) of temperature given a current of anywhere from 400uA to 5mA (0.0004 to 0.0050 amps) flowing through it. Typically, you hook up a 2.2 kilo-ohm (2200ohms or 2K2ohm) resistor from the +5 volt regulated power supply to the positive ("+") pin of the LM335 and ground the negative ("-") side. The "ADJ" pin is not connected. The voltage on the positive pin will be 2.73 volts at 0'C and 2.98 volts at 25'C and so on. The spreadsheet embedded below shows some other examples. It's accuracy is about 1'C and it can operate from -40'C to 100'C. That is 212'F down to -40'F (yes, -40'C is -40'F). It's pretty cheap (around a buck^) and you can get it in a nice TO-92 case which can be stuck in heat shrink tubing to create a sealed temperature probe.

The accuracy of the sensor is just the first part of the accuracy story. In order to use any sensor with a uC (microcontroller), we have to convert the analog voltage into a digital number. The ADC (Analog to Digital Converter) in the uC can do that, but it does it by comparing that voltage with a voltage reference. The most basic reference voltage is the supply voltage. So if the power supply voltage isn't well regulated, it will throw off the reading. And, the ADC only has so many bits of accuracy which determines how finely the range of voltage is divided. For example, a 10 bit ADC divides the voltages between 0 and 5 volts into 1024 (2^10) slices, each being 4.883mV (0.004883 volts; 5/1024). So if it is 20'C (68'F) and the LM335 is dropping 2.93 volts and the +5 volt supply is really at 5.00 volts, then the ADC will read 600. That is 600*0.004883 = 2.93 volts in ADC counts. The spreadsheet embedded below shows some other examples.

The temperature can rise from 20'C to 20.5'C, and the LM335 can move from 2.930 to 2.935 volts before the ADC clicks over from 600 to 601. So you would think that best case accuracy is half a degree, and worst case, with a standard power regulator like the LM7805 putting out 4.98 to 5.02 volts, and the LM335 off by an entire degree, you can actually be a couple degrees off. But... it turns out you can do much better. How? Time and noise. Our enemies can be our friends. More on that later.

Before we can worry about accuracy, we need to get past converting the ADC counts into a displayable temperature in 'C or 'F. Putting 600 out on a display isn't going to tell the users that it's a little cold in the room. At 0'C, the ADC count is 559 so we can adjust for 0 by just subtracting 559. Since each ADC count represents 0.004883 volts and each 0.01 volt represents a 'C, we can convert to 'C by subtracting 559 from the count and then multiplying times 0.4883 (0.004883 / 0.01). Or by multiplying by 0.4883 first which gives about 273, and then subtracting 273 to get 0 at 0'C. Well educated students with good memories will remember 273 as the offset between 'K and 'C; the LM335 actually returns 'K. Well educated students with good memories may also remember Y=mX+b from Algebra. This is exactly that, were the m is 0.4883 and the b is -273. And that will work... but most uC's are hard pressed to do floating point operations (math with numbers that have digits right of the ".")

Integer math is much easier for a uC (smaller program uses less of the available memory and works faster) so a simple solution is to multiply the ADC count by 4883 and then just ignore the last few digits of the answer. So (600-559)*4883=200203 which you can read as 20'C if you just don't look at the last 4 digits. That also works, but 200203 is a big number, and at higher temperatures, like 60'C / 140'F when the ADC counts (681-559)*4883=595726 (close enough) the numbers need 3 bytes of storage. It takes 20 bits to store a number that big, and since they are parceled out in bytes that is 3 memory registers in the uC... 3 valuable memory registers. And most C compilers do math in 1 (char), 2 (short), or 4 (long) bytes chunks; they don't have math libraries for 3 byte values, so you would have to use a "long" and waste 4 bytes.

Wouldn't it be nice if we could multiply by say 4.883 (to get 'C times 10 then put the decimal point into the display between the ones and tens unit) without using floating point math and without using up 4 registers? Well, if we get really tricky, we can. There is a method of multiplying or dividing a number by any constant value, even fractional values, that doesn't use floating point... in fact, it doesn't even use multiplication or division... not in base 10 anyway. It uses binary shifting, which is built into just about every microcontroller, to multiply or divide by any multiple of 2, then adds or subtracts those operations to accumulate the equivalent of the original desired computation. It is fully documented at:
http://techref.massmind.org/techref/method/math/muldiv.htm
but the general idea is that since computers represent numbers in base 2, the way we represent numbers in base 10, just as it is very easy for us to multiply by 10 by just shifting the decimal place left, or divide by 10 by shifting it right, it is also very easy for computers to multiply or divide by 2.

A very clever guy put together all the known best ways of using this into a script that figures out how best to multiply or divide by any number, with any precision, with any allowable error. His program directly produces code for the PIC Microcontrollers in assembly language, but since it lists the method used, it's easy to translate that into C or any programming language that supports shifts. If your C compiler optimizes multiplication and division by powers of 2 into shifts, you don't even have to do that part (sadly, most low end or free versions do not). The script is hosted online at:
http://www.piclist.com/techref/piclist/codegen/constdivmul.htm
go check it out!

"If you put in 16 bits as the register size (a short in C) and 4.88281 as the constant (including a *10 of the actual value so we can get one digit right of the decimal with integers), and press ""Generate code"" you get back:

; ACC = ACC * 4.88281
; Temp = TEMP
; ACC size = 16 bits
; Error = 0.5 %
; Bytes order = little endian
; Round = no

; ALGORITHM:
; Clear accumulator
; Add input * 4 to accumulator
; Add input * 1 to accumulator
; Substract input / 8 from accumulator
; Move accumulator to result
;
; Approximated constant: 4.875, Error: 0.16 %

followed by a bunch of PIC assembly code which you can ignore. The part you want is under "ALGORITHM" and it basically shows that you should take the ADC counts (call them "a") and multiply by 4 then add the that to the original value of a then "substract" (he isn't good at spelling) the original value of a divided by 8. To put it mathematically: 10c = 4a + a - a/8 -2729 or programmatically cten = a*4 + a - a/8 -2729.

Now, a good C compiler should translate that into very, very short, efficient code because for a microcontroller, multiplying by 4 just means shifting left twice and dividing by 8 is shifting right three times. But you can make sure your compiler does it the easy way by using the << (shift left) and >> (shift right) operators with the number of bit positions instead of the multiplier. So that would be: cten= (a<<2) + a - (a>>3) - 2729. On most 8 bit microcontrollers that will compile to about 40 instructions which will execute right through (no loops) vs several hundred instructions and more cycles if a regular integer multiply and divide are used.

The spreadsheet has some other related conversion like 'C to 'F and ADC count direct to 'F by floating point and binary methods. As you can see if you check carefully, the answers don't always come out perfectly, but in general, they are more than close enough, especially considering the error inherent in the sensor.

Now, back to accuracy. Any analog system will suffer from noise, meaning that your sensor won't put out exactly 2.73 volts when it should; one instant it will be putting out 2.733 and the next it might be putting out 2.729. The value will bounce around for many /many/ different reasons, some of which are documented along with ways of avoiding noise. But you can't really avoid it completely. As a programmer in an embedded environment, you must learn to deal with the noise in your software. The most common method is filtering, and the most common filter is just a simple running average. What this means is that you take, not one, but several samples, and each sample is averaged in with the prior samples. The average of your last so many samples over time is much more stable, and much more accurate, than any single sample could hope to be. Everyone should know how to do an average: Just add up the numbers, and divide by the number of numbers. But a running average requires a bit of thought. You could just keep the last so many reading separately, and average them each time. Or... you can take the first reading, multiply it by the number of samples over which you wish to average minus 1 and then add in the new sample, and divide the total by the number of samples.

For example, if you want an average over the last 16 samples, you could do this: a = (a*15 + n)/16 If you think about that for a while, it will makes sense. The single average value, a, is being multiplied by 15, which gives it the magnatude of 15 prior samples added together. Then the n, added into that, gives us 16 numbers in total, which we divide by 16 to complete the average.

Notice I picked 16 samples. 16 is a power of 2, so dividing by 16, inside a microcontroller, is just shifting right 4 times. And a lot of microcontrollers have a nibble swap instruction which can be used to do those 4 shifts in 2 operations. Isn't it too bad that we have to multiply by 15? Ah... but wait! Multiplying by 15 is just the same as multiplying by 16 and subtracting 1! Our running average of the last 16 values becomes:

a = ((a<<4) - a + n)>>4; //remember, <<4 is times 16 and >>4 is divide by 16.

This actually works quite well, however, Roman was kind enough to point out that it can be done with less math and greater accuracy. Storing the value that you have divided by 16 reduces the overal accuracy of the average, because we are using non-floating point math; we are loosing the fractional part of the total each time. To compensate, you could just keep the sum, without dividing by 16, then each time you take a new sample, subtract out one sixteenth of the current sum as your result, and add the new sample. This requires an extra variable to output a result (call it "r") but improves the resolution of the running total and actually requires a bit less math (no <<4).

// a = accumulator (is always 16* larger than a sample)
// n = new sample
// r = result (for output)
r = (a>>4);	// output result is 1/16th of accumulator
a -= r;   // subtract l/16th of the accumulator
//In the C programming language, a -= r is the same as saying a = a - r.
a += n;     // add in the new sample

Our complete program to read the ADC input from the LM335, convert it to 'C and then to 'F and average that value over the last 16 readings becomes:

while (1) { // loop forever
 	k = (adc<<2) +adc -(adc>>3) +(adc>>7);  // *4.883 0.0038% err
 	c = k-2755; // offset from Kelvin to C
 	f = (c<<1) -(c>>2) +(c>>5) +(c>>6) +320; //convert from C to F
	r = (a>>4);	// output result is 1/16th of accumulator
	a -= r;   // subtract l/16th of the accumulator
	a += f;     // add in the new sample
 	printf ("temperature: %4.1f'F\n", r/10); // divide by ten to convert to floating point (terrible but just for now)
 	__delay_ms(100); //wait for a bit
 	}; //do it again

That printf is a right horror, as there are much better ways to convert a 16 bit value from binary to decimal, but that is a subject for another day. A day with a bottle of asprin handy.

If you have the chance to watch this code run, and very carefully change the input value from the sensor, you will notice something interesting. The display will show values like 69.2'F. And a slight increase in temperature will show 69.3'F. How is that possible when each ADC count is almost half a degree? As the spreadsheet below shows, moving from 600 to 601 should change the display from 67.9 to 68.8! You can't read 600.5 ADC counts, yet the system seems to be doing it. What is happening is that our enemy noise has become our friend. The ADC value is randomly hopping around, due to noise, and sometimes it is giving us 600 and sometimes 601. If the actual temperature is 68.5, then the reading will be 600 about half the time, and 601 the other half. The average between the resulting 'F outputs of 67.9 and 68.8 is giving us a display reading of 68.3! Not perfect, but much better than expected. When the temp is 68.7, it will get 600 a quarter of the time and 601 the other three quarters. And so on...

In reality, the input will sometimes jump two full ADC counts high, or even 3 low, and you will see slight changes in the display value even when the temperature isn't actually changing at all. But over all, the average value will center around the actual, perfectly accurate, true temperature. And that is the beauty of design.

This spreadsheet shows some sample values of temperatures in 'C and 'F, and then the voltage produced by the LM335 and the ADC reading you would expect with a 10 bit A2D converter and a +5 volt reference. Next it shows the results of the different methods discussed here.

The page dedicated to my son, Remy, and my daughter, Allie, for whom it was written. I hope it explains how things work, why things are more complex than they seem, math is your friend, and how problems can be turned to your advantage.

Notes:

Conversion from C to F isn't really discussed, because it's just another mX+b conversion, and can be done in the same way. Actually, if all you want is 'F as the final output, there is no point in going from ADC counts to 'C, then from 'C to 'F, you can just go directly. There are some samples in the spreadsheet that show how to do that. Converting to 'C and then from that to 'F gives you the option of displaying either for the end user; just add some way for the users to select which one they want, and then use that one. Roman provided a nice, quick direct to 'F formula: 'F = (ADC - constant) *139 /256 which works very nicely with integer math and short (16 bit) variables.
The code was written for a PIC16F690 running on the PIC BOB PCB with an LCDPanel1

Comments:

Mohit Mahajan
And if I've understood it right, you NEED noise for improved resolution of display.
An application note from Atmel (AVR121) also shows how noise could be used to increase ADC resolution by oversampling.
- Mohit Mahajan.

Also:

Remote LM335 Sensor Electronics

Micro controller interfacing to analog sensors (such as the LM335A Temperature Sensor)

by James Newton

Welcome to www.piclist.com!

Micro controller interfacing to analog sensors
(such as the LM335A Temperature Sensor)