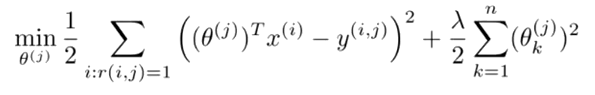
The obvious examples are web services that sell movies, music, books, or other products. Based on what each customer has purchased, or the ratings they gave, recommend new items that the user is likely to purchase or rate highly. Ratings are often over a range (e.g. 0 to 5 stars) and may not be available for all products purchased / used. The products first need to be grouped or classified, and then we can look for patterns in each users ratings / consumption. E.g. Mary Jane loves romantic movies, but Billy Bob likes action flicks. Now, given that a movie neither has yet seen is a romantic comedy, what rating is MJ likely to give it? How about BB?
So we can treat this as a combination of a Classifier (possibly using clustering if we don't have known classes) which finds parameters for each product and a Linear Regression predictor to learn the users preferences.
We have:
We need to predict the rating of each product i, which they haven't rated
as (o(j))Tx(i). Both
o(j) and x(i) are vectors of k+1 elements
where k is the number of classes. Note: The +1 is because of the unit
vector x0 which is always 1.
As with the standard Linear Regression,
to learn o(j) we find the minimum values for
the sum, over the values of i where r(u,p) is set,
of (o(j)Tx(i) -
y(i,j))2 divided by 2. We don't divide by the number
of products rated, m(j), because that number will be different
for each parameter. We also should add
Regularization of 1/2 lambda over the k
classes. Here is that cost function:
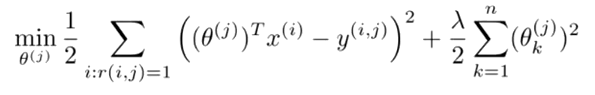
The slope function is: (but remember to omit the lambda term for k=0)
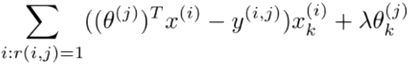
We repeat this for all users from 1:nu
Known o, unknown x: Another version of this has no
classifications for the product, but the users have provided labels for what
sort of products they like. In other words,
o(j) is provided and we don't have
x(i). We do have the y(i,j) ratings for each product
that was rated by each user. Based on this, we can guess what the x values
will be and then use that to predict the y values for unrated products. In
this case, we can use exactly the same method as above, except that we will
change x and find the minimum cost for x, over all the users instead of all
the products j:r(i,j)=1, while also using
regularization for x instead of
o.
Back and forth: If we have neither the x values or the
o values, we can randomly guess o, and
use that to develop some x values, then use those values to develop better
o values and by working back and forth, between the two
different parameter sets.
Both x and o unknown: And, in fact, we can combine
the two versions of the cost function (with
regularization for both x and
o) and minimize for both x and o over all
users and products (i,j):r(i,j)=1, resulting in a single Linear Regression
problem which solves for both x and o at once. We start
by initialize all the values of x and o to small random
numbers much like we do for Neural Nets and
for the same reason: This serves to break symmetry and ensures the system
learns features that are different from each other.
x0=1 not needed: An interesting side effect of this combined
learning of both x and o is that we no longer need
x0=1. And the reason is completely amazing: Because the system
is learning all the X's, if it wants an x which is 1, it will learn one.
... {ed: pause to let brain explode and re-grow}. We can now regularize
all x and o parameters.
After we have a matrix x of product attributes, we can find products which are related simply by finding those with simular values of x.
If we take a matrix, Y, of all the product ratings (products x users
or np x nu) with gaps where some users haven't rated
some products, we can attempt to fill in those gaps. We can also make predictions
for each element to see if we are making good predictions against the known
values. Element Y(1,1) is
O(1)Tx(1). If we take all the X values,
x(1) ... x(np), transpose, and stack them
into a vector, then do the same with O, we can compute our
prediction for Y = X·OT. In
Octave must as we did for
Linear Regression
% X - num_movies x num_features matrix of movie features % Theta - num_users x num_features matrix of user features % Y - num_movies x num_users matrix of user ratings of movies % R - num_movies x num_users matrix, where R(i, j) = 1 if the % i-th movie was rated by the j-th user %Compute Cost hyp = (X*Theta'); errs = (hyp - Y); err = errs .* R; %note .* R removes unrated J = sum(err(:).^2)/2; %note not dividing by m %Regularization (both Theta and X) J = J + (lambda .* sum(Theta(:).^2) ./ 2); J = J + (lambda .* sum(X(:).^2) ./ 2); %Note that there is no need to remove the first element %Compute X gradient with respect to Theta for i=1:num_movies; %for each movie idx = find(R(i, :)==1); %list of users who rated this movie Thetatemp = Theta(idx, :); %Theta features for these users Ytemp = Y(i, idx); %Ratings by these users X_grad(i, :) = (X(i, :) * Thetatemp' - Ytemp) * Thetatemp; endfor % Or in matrix form: X_grad = (err * Theta) + (X .* lambda); %Compute Theta gradient with respect to X for j=1:num_users; %for each user idx = find(R(:, j)==1); %list of movies rated by this user Xtemp = X(idx,:); %X features for these movies Ytemp = Y(idx, j)'; %Ratings for these movies, %Note this is transposed to a column of movie ratings Theta_grad(j, :) = (Theta(j, :) * Xtemp' - Ytemp) * Xtemp; endfor % Or in matrix form: Theta_grad = (err' * X) + (Theta .* lambda);
When a user has not rated any products, our minimization system will develop
all zero values for o, which is not useful. We can use Mean
Normalization to develop average ratings for each product which I can assign
as a new users expected ratings.
| file: /Techref/method/ai/Recommenders.htm, 8KB, , updated: 2015/9/15 14:25, local time: 2025/10/22 21:02,
216.73.216.114,10-3-244-150:LOG IN
|
| ©2025 These pages are served without commercial sponsorship. (No popup ads, etc...).Bandwidth abuse increases hosting cost forcing sponsorship or shutdown. This server aggressively defends against automated copying for any reason including offline viewing, duplication, etc... Please respect this requirement and DO NOT RIP THIS SITE. Questions? <A HREF="http://www.piclist.com/techref/method/ai/Recommenders.htm"> Prediction / Recommendation Systems.</A> |
| Did you find what you needed? |
|
o List host: MIT, Site host massmind.org, Top posters @none found - Page Editors: James Newton, David Cary, and YOU! * Roman Black of Black Robotics donates from sales of Linistep stepper controller kits. * Ashley Roll of Digital Nemesis donates from sales of RCL-1 RS232 to TTL converters. * Monthly Subscribers: Gregg Rew. on-going support is MOST appreciated! * Contributors: Richard Seriani, Sr. |
Welcome to www.piclist.com! |
.