 Radix Radix
 In the software of the computer, hexadecimal is often used. In the software of the computer, hexadecimal is often used.
 Decimal Decimal
In our daily life, 10 numbers from "0" to "9" are used.
In case of the count-up, after 9, the carry is done and becomes 10. We are using properly but this is the count method of the number which the human being decided.
This seems to depend on that the fingers of the hand of the person is 10.
 Binary Binary
Only two values of "0" and "1" are used to express a condition by the digital world which included a computer. These are sometimes expressed by "Low level " and "High level ", too.
Like 0 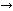 1 1 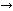 10, after 1, it is 10. 10, after 1, it is 10.
 Hexadecimal Hexadecimal
In the condition to be handling with the computer, it is a binary number but it is difficult to understand for the person who is using the decimal.
163(Decimal) 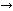 10100011(Binary) 10100011(Binary)
Therefore, a hexadecimal is used as the expression which it is easy for the person to understand. As for the hexadecimal, 16 numbers are used for 1 digit. It is from 0 to 9 that it is expressed by the figure. So, six of the remainder are expressed by the alphabet.
10 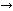 A, 11 A, 11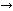 B, 12 B, 12 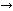 C, 13 C, 13 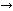 D, 14 D, 14 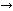 E, 15 E, 15  F F
The figure has begun with 0. Therefore, 10 of the figure shows the 11th and 15 shows the 16th.
16 kinds of conditions are expressed by 4 bits in the binary. Oppositely, the hexadecimal is used because that it is possible to express 16 by 4 bits. There is the octal which is expressed by 3 bits. In case of the hexadecimal, 1 byte is expressed by 2 digits.
Also, it puts "h" to distinguish the hexadecimal from the decimal. h is the initial of hexadecimal(16).
It shows in 00h or H'00' or 0x00. However, an expression isn't unified.
 The correspondence of radix The correspondence of radix
The correspondence of Binary, Decimal and Hexadecimal is as follows.
| Decimal | Binary | Hexdecimal |
| Decimal | Binary | Hexdecimal |
| 0 | 0 | 0h | 100 | 1100100 | 64h |
| 1 | 1 | 1h | 127 | 1111111 | 7Fh |
| 2 | 10 | 2h | 128 | 10000000 | 80h |
| 3 | 11 | 3h | 200 | 11001000 | C8h |
| 4 | 100 | 4h | 255 | 11111111 | FFh |
| 5 | 101 | 5h | 256 | 100000000 | 100h |
| 6 | 110 | 6h | 300 | 100101100 | 12Ch |
| 7 | 111 | 7h | 400 | 110010000 | 190h |
| 8 | 1000 | 8h | 500 | 111110100 | 1F4h |
| 9 | 1001 | 9h | 511 | 111111111 | 1FFh |
| 10 | 1010 | Ah | 512 | 1000000000 | 200h |
| 11 | 1011 | Bh | 600 | 1001011000 | 258h |
| 12 | 1100 | Ch | 700 | 1010111100 | 2BCh |
| 13 | 1101 | Dh | 800 | 1100100000 | 320h |
| 14 | 1110 | Eh | 900 | 1110000100 | 384h |
| 15 | 1111 | Fh | 1000 | 1111101000 | 3E8h |
| 16 | 10000 | 10h | 1023 | 1111111111 | 3FFh |
| 17 | 10001 | 11h | 1024 | 10000000000 | 400h |
| 18 | 10010 | 12h | 2000 | 11111010000 | 7D0h |
| 19 | 10011 | 13h | 2047 | 11111111111 | 7FFh |
| 20 | 10100 | 14h | 2048 | 100000000000 | 800h |
The change of Binary, Decimal and Hexadecimal can make simple if you use the function electronic calculator which is attached to the Windows.
When changing without using the calculator, it is possible to do in the following way.
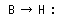 |
It is possible to change simply if dividing 4 bits.
It is easier if learning a binary pattern to Fh from Ah.
EX. 111000100100010000100  1C4884h 1C4884h |
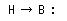 |
It is possible to change 1 digit of the hexadecimal into the binary in the order.
EX. 5F37Bh 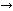 1011111001101111011 1011111001101111011 |
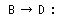 |
This is troublesome a little.
First, you write a decimal value every bit like the following figure. Total the decimal value of the bit of "1".
EX.
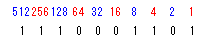
512 + 256 + 128 + 8 + 4 + 1 = 909 |
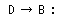 |
This is terrible a little, too.
Subtract the maximum number of power of two(1,2,4,8,16,32,64,128,256,512,1024,...) which can be subtracted from the decimal number.
It makes the bit which corresponds to the number of power of two which could be subtracted to "1".
Subtract the number of power of two which could be subtracted from the remainder more.
Hereinafter, repeat similar subtraction until the remainder passes away.
The row of "1" and "0" by above result is a binary number.
EX. "582"
582 - 512 = 70
70 - 64 = 6
6 - 4 = 2
2 - 2 = 0
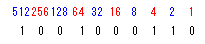 |
 |
Change a decimal into the binary first and change a result into the hexadecimal more.
In case of the example(D  B) which was shown above, 582 = 1001000110 = 246h. B) which was shown above, 582 = 1001000110 = 246h.
When changing directly, there is a way of dividing by the value of 4 bits.
582 / 256 = 2 remainder 70
70 / 16 = 4 remainder 6
The result is 246h. |
 |
Change a hexadecimal into the binary first and change a result into the decimal more.
In case of the example(B 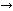 D) which was shown above, 38Dh = 1110001101 = 909 D) which was shown above, 38Dh = 1110001101 = 909
When changing directly, there is a way of multiplying the value of 4 bits.
3 x 256 = 768
8 x 16 = 128
The result is 768 + 128 + 13(Dh) = 909. |
Still, it is easy to calculate using the function electronic calculator.
 2's Complement 2's Complement
The 2's complement is the one which shows negative numerical value.
For example, "-1" of the decimal number is 11111111 when showing by the binary with byte.
It is as follows when confirming.
 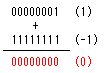 The overflow occurs but the numerical value becomes zero. The overflow occurs but the numerical value becomes zero.
A binary addition is done from the lower rank figure like the decimal number. When there is a carry, it calculates a higher rank figure including it.
To use a negative value, there is a condition.
The numerical value which it is possible to show at the byte is 256 kinds of 0 to 255. However, when using the negative value, it becomes 255 kinds of - 127 to +127. The reason why the numbers are few is because 10000000 isn't used. The row of these bits shows -0 but in the calculation, it can not use. Most significant bit 7 is used as the sign bit which shows negative or positive. The type with numerical value must be considered when processing it.
For example, it is 10000001 when showing -127 in the binary number. It becomes 129, supposing that this is only plus numerical value.
A change into the 2's complement is done as follows.
I attempt to change 56 into -56 as the example.
| (1) Subtract 1 from the value |  56 - 1 = 55 56 - 1 = 55 |
| (2) Change this into the binary |  55 55 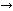 00110111 00110111 |
| (3) It makes 0 and 1 opposite |  00110111 00110111 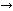 11001000 11001000 |
 11001000 is the binary number which shows -56. 11001000 is the binary number which shows -56.
It is as follows when confirming.
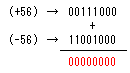
 The answer became zero. The answer became zero.
 General format for instructions General format for instructions
The format for instructions of PIC16 series is the following three kinds. The instructions are written in the program memory and one instruction is composed of 14 bits. These 14 bits are called a word.
 |  Byte-oriented file register operations Byte-oriented file register operations |
| The instructions of this format are the instructions which processes a byte unit. |
|  | 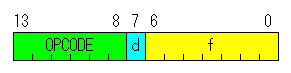 |
|  | OPECODE : | The code to distinguish a instruction is written. |
 |
| d (Destination select) : |
It specifies the register which stores the execution result of the instruction.
d=0 : It specifies working register ( W reg ).
d=1 : It specifies file register which is specified by f.
In case of the assembler language, d is written in W or F. |
|  (EX) (EX) | ADDWF | COUNT,W | ( d=0 when writing W ) |
| ADDWF | COUNT,F | ( d=1 when writing F ) |
 |
| f (Register file) : |
It specifies the address of the register which is dealt with for the instruction.
f can specify an address from 0(00h) to 127(7Fh) because it is 7 bits.
In case of PIC16F84A, because the register memory is 80 bytes including SFR, it is possible to be specified by f if being 7 bits.
When writing by the assembler language, the label is put to the register and uses. |
|  (EX) (EX) | ADDWF | COUNT,F | ( COUNT is the label of the register) |
|
 |
|  Bit-oriented file register operations Bit-oriented file register operations |
| The instructions of this format are the instruction which processes a bit unit. |
| 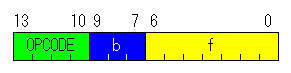 |
| OPECODE : | The code to distinguish a instruction is written. |
 |
| b (Bit address) : |
It specifies the bit position of the register file.
Because the register file is a byte, it can specify all bit positions with 3-bit b. |
 |
| f (Register file) : |
It specifies the address of the register which is dealt with for the instruction.
f can specify an address from 0(00h) to 127(7Fh) because it is 7 bits.
In case of PIC16F84A, because the register memory is 80 bytes including SFR, it is possible to be specified by f if being 7 bits.
When writing by the assembler language, the label is put to the register and uses. |
|
|
|
|
|
|
|
|
|
|  Literal and control operations Literal and control operations |
|
|
|
The instructions of this format do the processing which used the fixed number (k) which was written in the instruction.
There are two instruction types and fixed number (k) is 11 bits about GOTO and CALL instruction. |
|
|
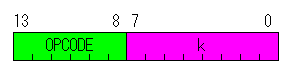
In case of GOTO and CALL instruction
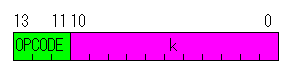 |
| OPECODE : | The code to distinguish a instruction is written. |
 |
| k (Literal field) : |
This is the fixed number to use for the calculation.
It specifies by the numerical value or the label.
Because it is a byte except JUMP and CALL instruction, it is the range of 0(00h) to 255(FFh).
Because GOTO or CALL instruction is 11 bits, it is the range of 0(00h) to 2047(7FFh). |
|
|
|
|
|
|
|
|
 |